3 Extrêmes, non-stationnarité et changements climatiques
L’un des impacts majeurs des changements climatiques est une modification de l’amplitude et de la fréquence de conditions météorologiques extrêmes, dont une intensification des précipitations extrêmes.
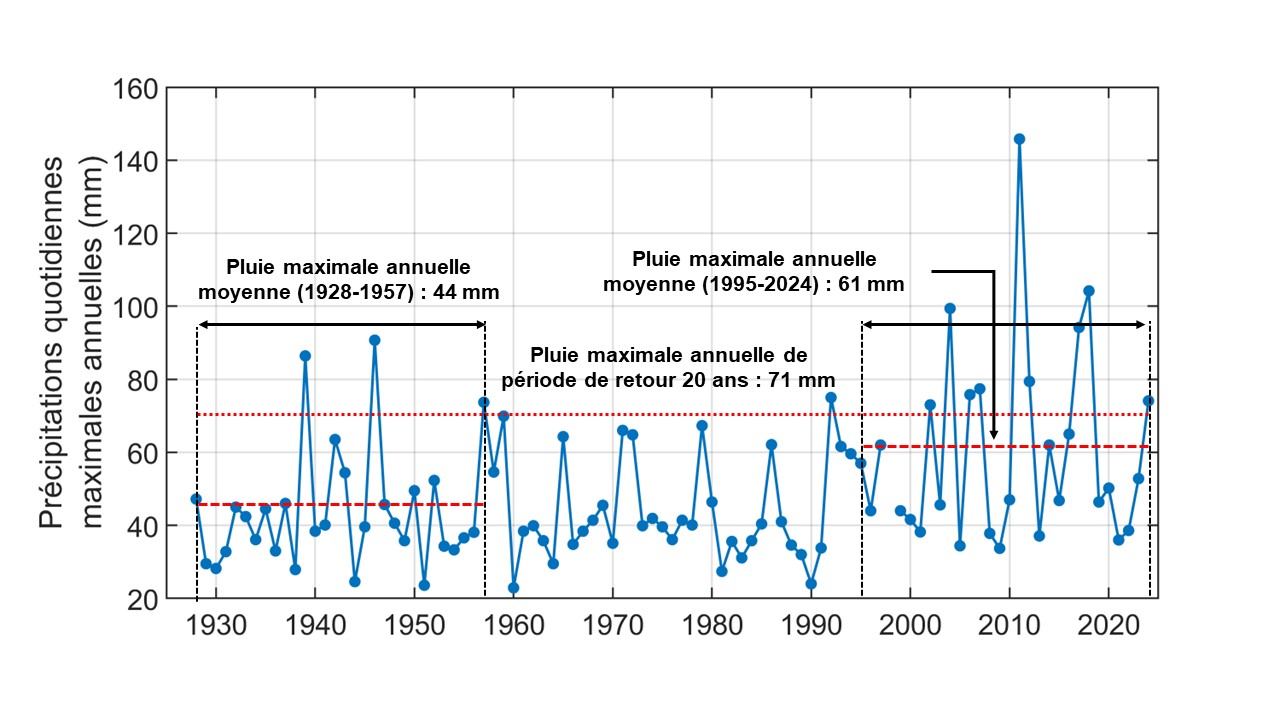
Reprenons l’exemple de la Figure 2.1 afin d’illustrer comment se manifestent les changements climatiques. On constate qu’au-delà de la grande variabilité interannuelle, les précipitations maximales annuelles semblent augmenter avec le temps. Ainsi, la moyenne sur les 30 premières années (1928–1957) est de 44 mm, alors que la moyenne pour les 30 dernières années (1995–2024) est de 61 mm (Figure 3.1). L’application d’un test statistique (test de Mann-Kendall au seuil de significativité de 95%; voir la fiche 6) confirme l’hypothèse d’une tendance à la hausse à cette station (p-value < 0.01). On parle alors de tendance statistiquement significative. Le taux de variation des précipitations extrêmes estimé pour la station de Chelsea est de 3.5 %/décennie1. Une telle série est dite non-stationnaire.
La tendance présentée à la Figure 3.1 est représentative des tendances parfois observées et généralement simulées par les modèles climatiques (hausse ou baisse progressive de la moyenne). Elle implique que la probabilité d’observer une valeur extrême supérieure à certains seuils augmente avec le temps. Considérons de nouveau la série de la Figure 3.1 et plaçons-nous en 2000. On peut estimer la précipitation maximale annuelle de période de retour2 20 ans à partir de la série disponible à ce moment (1928-2000), ce qui donne 71 mm.3 Pour les fins de l’exemple, supposons que cette valeur est utilisée pour la conception d’un ouvrage de capacité suffisante pour évacuer les eaux de ruissellement d’une pluie de 71 mm. Des dépassements de capacité, et donc d’éventuels bris de services, seraient susceptible de survenir en moyenne à tous les 20 ans, un seuil jugé raisonnable selon la tolérance au risque des concepteurs. Or, si on se reporte aux valeurs de la période 2001–2024, on constate que sa capacité aurait été dépassée neuf années4 pendant cette période, alors que quatre années avec des dépassements sont observées pendant la période 1928–2000. Le risque encouru pendant la période 2001–2024 va bien au-delà de celui initialement établi sur la base de la série ‘historique’. Cet exemple montre l’importance d’intégrer les changements climatiques dans la conception d’ouvrages.
Le taux de variation des précipitations maximales annuelles a été estimé à l’aide de la pente de Sen aussi appelée pente de Theil-Sen.↩︎
La période de retour correspond au nombre moyen d’années séparant deux années d’occurrence consécutives de ces pluies. La probabilité annuelle de dépassement p correspondant à une période de retour T est p = 1/T.↩︎
Cette valeur a été obtenue après ajustement d’une loi de Gumbel à la série de 1928 à 2000 (voir la fiche 7).↩︎
On présume que la capacité est dépassée une fois par année mais il n’est pas exclu qu’elle puisse être dépassée plus d’une fois certaine année.↩︎